Publications

2025

1. 

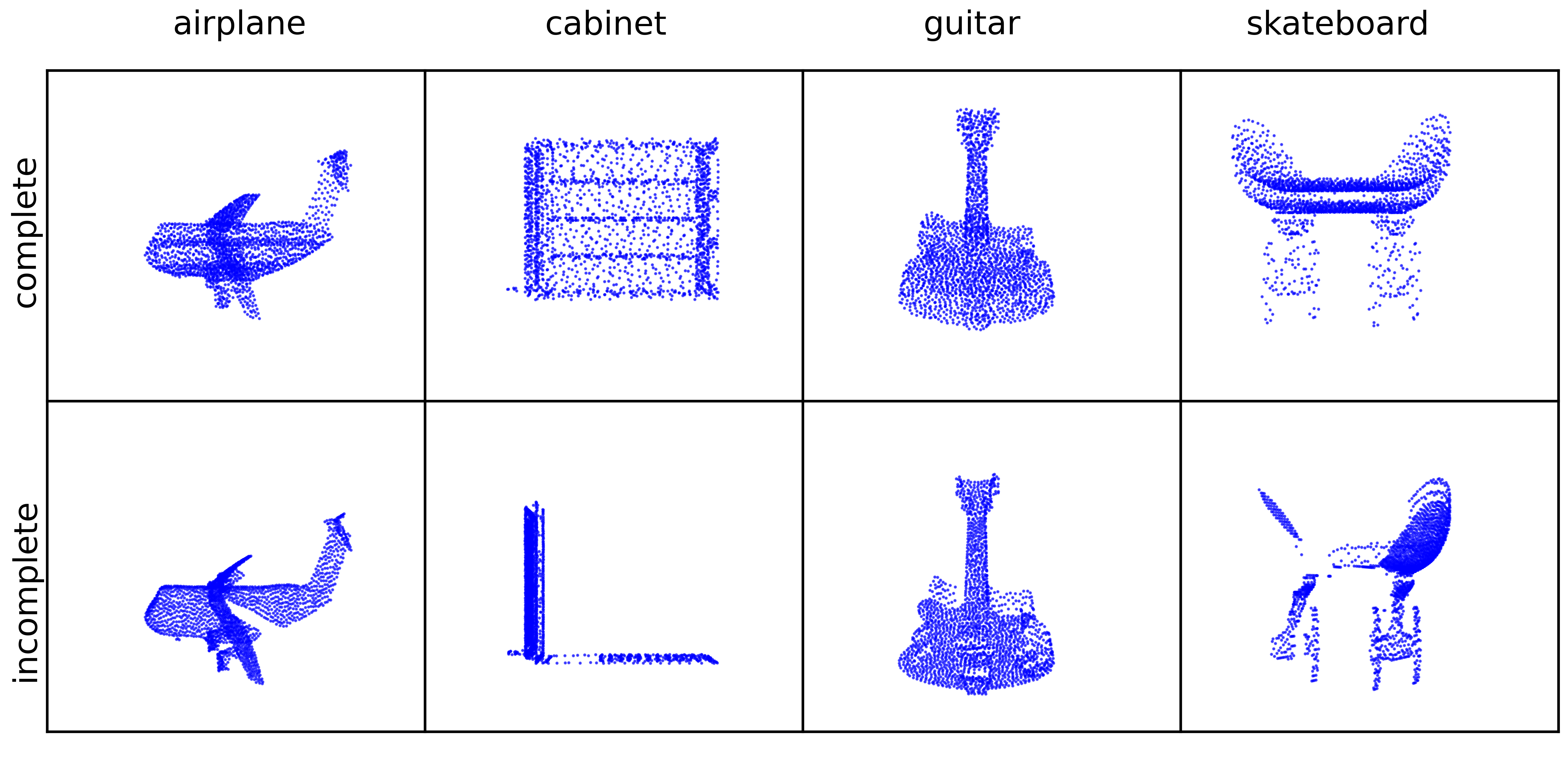   Linear Partial Gromov-Wasserstein Embedding

   Yikun Bai, Abihith Kothapalli^*, Hengrong Du^*, and 2 more authors

   International Conference on Learning Representations (ICLR), 2025

   Abs arXiv Poster

   The Gromov–Wasserstein (GW) problem, a variant of the classical optimal transport (OT) problem, has attracted growing interest in the machine learning and data science communities due to its ability to quantify similarity between measures in different metric spaces. However, like the classical OT problem, GW imposes an equal mass constraint between measures, which restricts its application in many machine learning tasks. To address this limitation, the partial Gromov-Wasserstein (PGW) problem has been introduced, which relaxes the equal mass constraint, enabling the comparison of general positive Radon measures. Despite this, both GW and PGW face significant computational challenges due to their non-convex nature. To overcome these challenges, we propose the linear partial Gromov-Wasserstein (LPGW) embedding, a linearized embedding technique for the PGW problem. For K different metric measure spaces, the pairwise computation of the PGW distance requires solving the PGW problem \mathcalO(K^2) times. In contrast, the proposed linearization technique reduces this to \mathcalO(K) times. Similar to the linearization technique for the classical OT problem, we prove that LPGW defines a valid metric for metric measure spaces. Finally, we demonstrate the effectiveness of LPGW in practical applications such as shape retrieval and learning with transport-based embeddings, showing that LPGW preserves the advantages of PGW in partial matching while significantly enhancing computational efficiency.

2. 

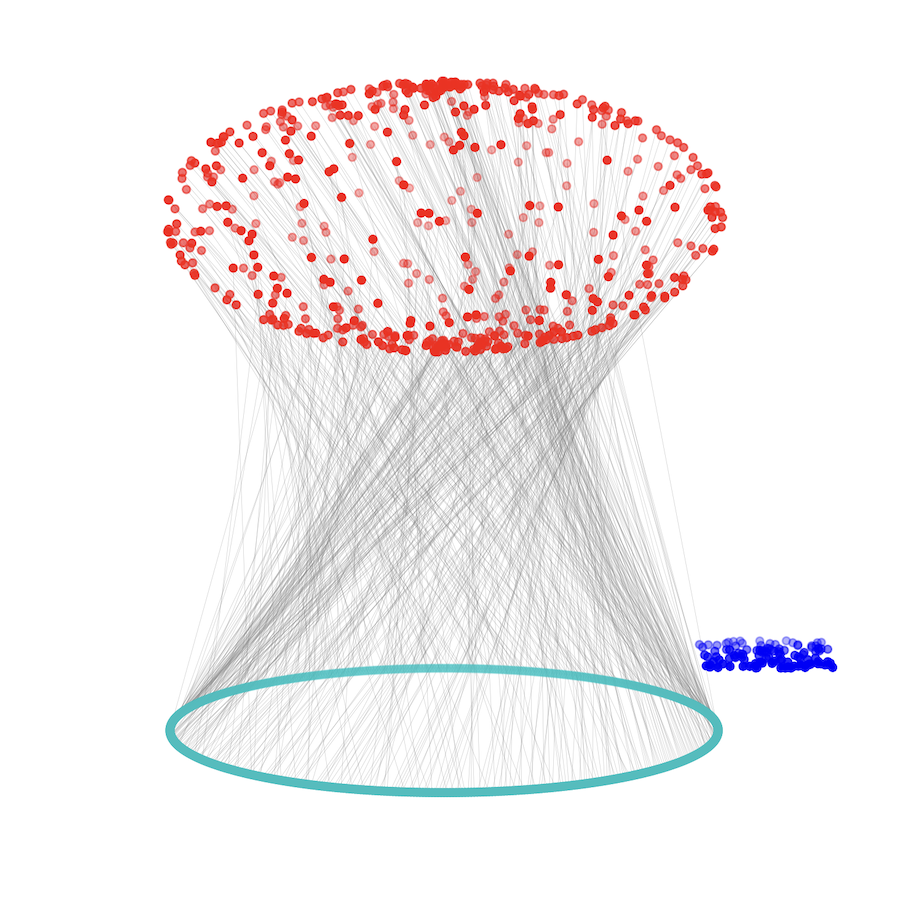   Partial Gromov-Wasserstein Metric

   Yikun Bai, Rocio Diaz Martin^*, Abihith Kothapalli^*, and 3 more authors

   International Conference on Learning Representations (ICLR), 2025

   Abs arXiv Poster

   The Gromov-Wasserstein (GW) distance has gained increasing interest in the machine learning community in recent years, as it allows for the comparison of measures in different metric spaces. To overcome the limitations imposed by the equal mass requirements of the classical GW problem, researchers have begun exploring its application in unbalanced settings. However, Unbalanced GW (UGW) can only be regarded as a discrepancy rather than a rigorous metric/distance between two metric measure spaces (mm-spaces). In this paper, we propose a particular case of the UGW problem, termed Partial Gromov-Wasserstein (PGW). We establish that PGW is a well-defined metric between mm-spaces and discuss its theoretical properties, including the existence of a minimizer for the PGW problem and the relationship between PGW and GW, among others. We then propose two variants of the Frank-Wolfe algorithm for solving the PGW problem and show that they are mathematically and computationally equivalent. Moreover, based on our PGW metric, we introduce the analogous concept of barycenters for mm-spaces. Finally, we validate the effectiveness of our PGW metric and related solvers in applications such as shape matching, shape retrieval, and shape interpolation, comparing them against existing baselines.

2024

1. Spotlight

   

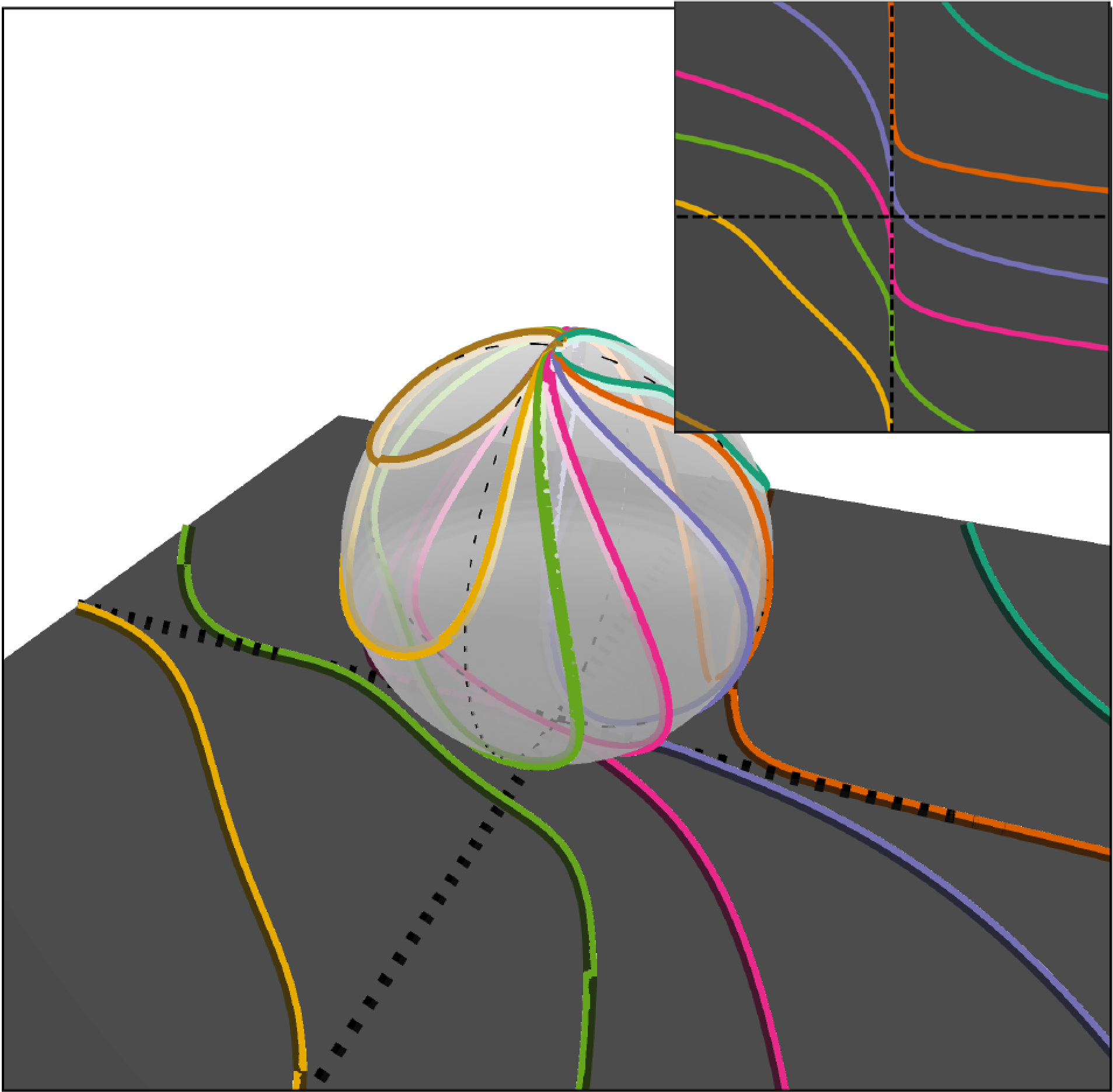   Stereographic Spherical Sliced Wasserstein Distances

   Huy Tran^*, Yikun Bai^*, Abihith Kothapalli^*, and 4 more authors

   International Conference on Machine Learning (ICML), 2024

   Spotlight Presentation [Top 3.50%]

   Abs arXiv Code Poster Website

   Comparing spherical probability distributions is of great interest in various fields, including geology, medical domains, computer vision, and deep representation learning. The utility of optimal transport-based distances, such as the Wasserstein distance, for comparing probability measures has spurred active research in developing computationally efficient variations of these distances for spherical probability measures. This paper introduces a high-speed and highly parallelizable distance for comparing spherical measures using the stereographic projection and the generalized Radon transform, which we refer to as the Stereographic Spherical Sliced Wasserstein (S3W) distance. We carefully address the distance distortion caused by the stereographic projection and provide an extensive theoretical analysis of our proposed metric and its rotationally invariant variation. Finally, we evaluate the performance of the proposed metrics and compare them with recent baselines in terms of both speed and accuracy through a wide range of numerical studies, including gradient flows and self-supervised learning.

2. 

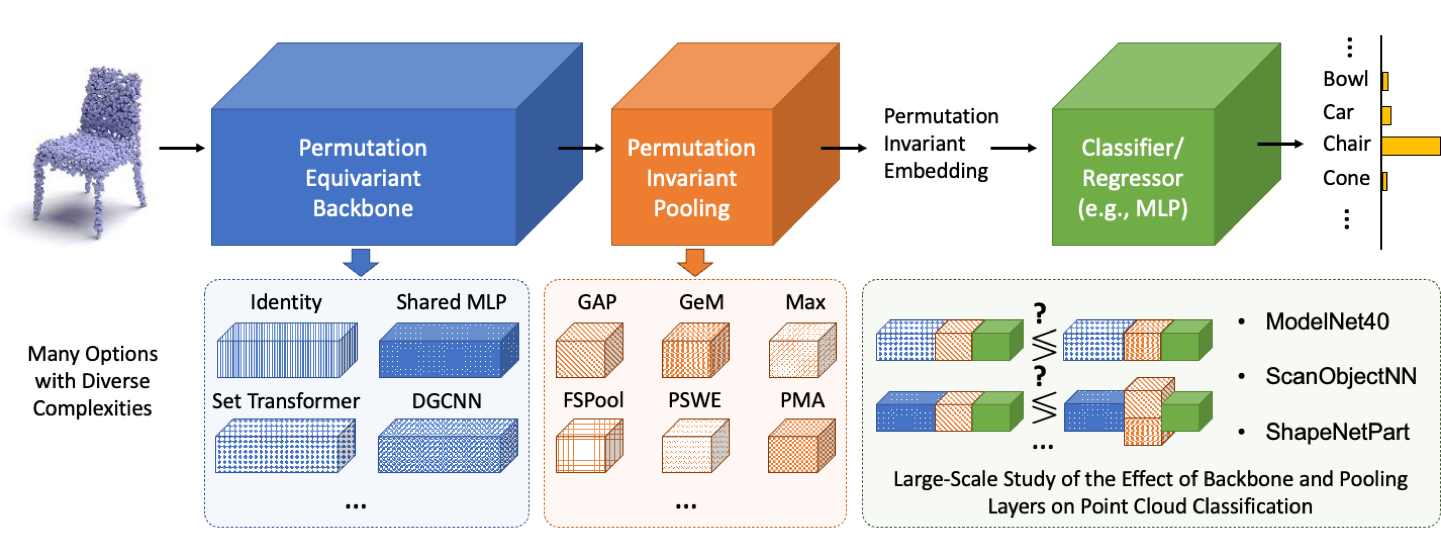   Equivariant vs. Invariant Layers: A Comparison of Backbone and Pooling for Point Cloud Classification

   Abihith Kothapalli, Ashkan Shahbazi, Xinran Liu, and 2 more authors

   International Conference on Machine Learning (ICML) Geometry-grounded Representation Learning and Generative Modeling Workshop, 2024

   Abs arXiv Code Poster

   Learning from set-structured data, such as point clouds, has gained significant attention from the machine learning community. Geometric deep learning provides a blueprint for designing effective set neural networks that preserve the permutation symmetry of set-structured data. Of our interest are permutation invariant networks, which are composed of a permutation equivariant backbone, permutation invariant global pooling, and regression/classification head. While existing literature has focused on improving equivariant backbones, the impact of the pooling layer is often overlooked. In this paper, we examine the interplay between permutation equivariant backbones and permutation invariant global pooling on three benchmark point cloud classification datasets. Our findings reveal that: 1) complex pooling methods, such as transport-based or attention-based poolings, can significantly boost the performance of simple backbones, but the benefits diminish for more complex backbones, 2) even complex backbones can benefit from pooling layers in low data scenarios, 3) surprisingly, the choice of pooling layers can have a more significant impact on the model’s performance than adjusting the width and depth of the backbone, and 4) pairwise combination of pooling layers can significantly improve the performance of a fixed backbone. Our comprehensive study provides insights for practitioners to design better permutation invariant set neural networks.

2023

1. 

   Learning-Based Heuristic for Combinatorial Optimization of the Minimum Dominating Set Problem using Graph Convolutional Networks

   Abihith Kothapalli, Mudassir Shabbir, and Xenofon Koutsoukos

   Under Review, 2023

   Abs arXiv Code Poster

   A dominating set in a graph is a subset of its vertices such that each vertex in the graph is either in the set or has a neighboring vertex in the set. The minimum dominating set problem seeks to find a dominating set of minimum cardinality and is a well-established NP-hard combinatorial optimization problem. We propose a novel learning-based heuristic approach to compute solutions for the minimum dominating set problem. Our approach uses a graph convolutional network to generate a series of probability maps over the vertices in a given problem instance, and we then treat these maps as heuristic functions to construct dominating sets. We conduct an extensive experimental evaluation of the proposed method on a novel synthetic graph dataset, real-world graph datasets, and existing minimum dominating set benchmark datasets. Our results indicate that the proposed learning-based approach can outperform a classical greedy approximation algorithm. Furthermore, we demonstrate the generalization capability of the graph convolutional network across datasets and its ability to scale to graphs of higher order than those on which it was trained. Finally, we utilize the proposed learning-based heuristics in an iterated greedy algorithm, achieving state-of-the-art performance in the computation of dominating sets.

2021

1. 

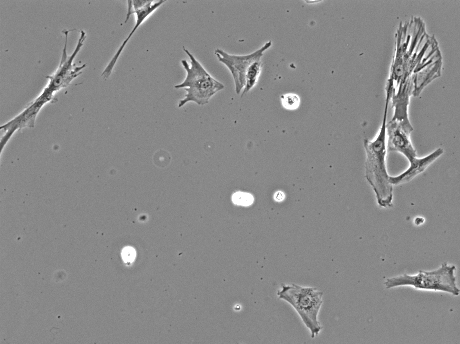   Supervised Machine Learning for Automated Classification of Human Wharton’s Jelly Cells and Mechanosensory Hair Cells

   Abihith Kothapalli, Hinrich Staecker, and Adam J. Mellott

   PLOS ONE, 2021

   Abs HTML PDF Code

   Tissue engineering and gene therapy strategies offer new ways to repair permanent damage to mechanosensory hair cells (MHCs) by differentiating human Wharton’s Jelly cells (HWJCs). Conventionally, these strategies require the classification of each cell as differentiated or undifferentiated. Automated classification tools, however, may serve as a novel method to rapidly classify these cells. In this paper, images from previous work, where HWJCs were differentiated into MHC-like cells, were examined. Various cell features were extracted from these images, and those which were pertinent to classification were identified. Different machine learning models were then developed, some using all extracted data and some using only certain features. To evaluate model performance, the area under the curve (AUC) of the receiver operating characteristic curve was primarily used. This paper found that limiting algorithms to certain features consistently improved performance. The top performing model, a voting classifier model consisting of two logistic regressions, a support vector machine, and a random forest classifier, obtained an AUC of 0.9638. Ultimately, this paper illustrates the viability of a novel machine learning pipeline to automate the classification of undifferentiated and differentiated cells. In the future, this research could aid in automated strategies that determine the viability of MHC-like cells after differentiation.